Dynamic flexible job-shop scheduling by multi-agent reinforcement learning with reward-shaping
Zhang L, Yan Y, Yang C, et al. Dynamic flexible job-shop scheduling by multi-agent reinforcement learning with reward-shaping[J]. Advanced Engineering Informatics, 2024, 62: 102872.
Abstract
Achieving mass personalization presents significant challenges in performance and adaptability when solving dynamic flexible job-shop scheduling problems (DFJSP). Previous studies have struggled to achieve high performance in variable contexts. To tackle this challenge, this paper introduces a novel scheduling strategy founded on heterogeneous multi-agent reinforcement learning. This strategy facilitates centralized optimization and decentralized decision-making through collaboration among job and machine agents while employing historical experiences to support data-driven learning. The DFJSP with transportation time is initially formulated as heterogeneous multi-agent partial observation Markov Decision Processes. This formulation outlines the interactions between decision-making agents and the environment, incorporating a reward-shaping mechanism aimed at organizing job and machine agents to minimize the weighted tardiness of dynamic jobs. Then, we develop a dueling double deep Q-network algorithm incorporating the reward-shaping mechanism to ascertain the optimal strategies for machine allocation and job sequencing in DFJSP. This approach addresses the sparse reward issue and accelerates the learning process. Finally, the efficiency of the proposed method is verified and validated through numerical experiments, which demonstrate its superiority in reducing the weighted tardiness of dynamic jobs when compared to state-of-the-art baselines. The proposed method exhibits remarkable adaptability in encountering new scenarios, underscoring the benefits of adopting a heterogeneous multi-agent reinforcement learning-based scheduling approach in navigating dynamic and flexible challenges.
Introduction
Given two sub-problems within DFJSP, scholars have formulated two types of heuristic rules for machine allocation and job sequencing. Current learning-based scheduling methods confront significant hurdles that compromise their effectiveness:
(1) In the single-agent paradigm, the action space grows exponentially with the scale of the problem. In multi-agents paradigms, multiple agents engage in decision-making at a joint decision point. Due to the intervals necessary for transportation between machines, decision processes regarding machine allocation and job sequencing for DFJSP occur at disparate moments.
(2) The feedback is only rendered after completing the final operation of each job, rendering it unperceivable at each decision milestone. It culminates in sparse reward challenges when employing the objective as a reward, thereby complicating learning processes.
(3)Training of DRL algorithms across variable problem sizes introduces significant differences in complexity. Thus, a critical demand exists for the innovation of versatile neural network architectures that adapt to variations in problem magnitude, thereby preventing the unnecessary demand for retraining in different scenarios.
Introduction
As a result this paper introduces three significant contributions:
(1) A multi-agent-based scheduling framework. This innovative framework encourages cooperation among the heterogeneous agents responsible for jobs and machines, steering them toward a unified goal. It simplifies the action space, significantly reduces computational complexity, and offers scalable solutions. These solutions can adjust to job and machine dimensions variation, with each agent independently managing its tasks.
(2) Multi-agent partial observation Markov Decision Processes (POMDP). These processes directly assign rewards enhanced with a reward-shaping mechanism based on the optimization objective, thus improving learning accuracy. This method makes substantial progress over traditional reward functions by removing the need to design manual and problem-specific reward functions.
(3) A multi-agent dueling double deep Q-Network Algorithm. It integrates the multi-agent scheduling framework with a dueling neural network architecture and a constrained action space. The result is highly adaptable and scalable decision-making Q-functions capable of addressing variable problem sizes in dynamic scheduling environments.
Problem formulation
A series of dynamic jobs, denoted by $J = \left{J_1,J_2,\ldots,J_n\right}$, arrive at the system at different times, defined by $at_i$. Each job, $J_i$, comprises several operations that must be processed according to a predetermined processing route, defined by $O_i = \left{O_{ij}\mid O_{i1},O_{i2},\ldots,O_{iNoi}\right}$. A set of machines, $M=\left{M_k \mid M_1, M_2, \ldots, M_m \right}$, offers processing services for these operations, where the processing time of $O_{ij}$ on $M_k$ is distinguished by $pt_{ijk}$. When two successive operations require processing on different machines, the transportation time is denoted by $tt_{k}^{k’}$.
The following assumptions are made to clarify the problem formulation:
• Machine breakdown is not considered.
• The processing buffer of each machine is unlimited.
• Transportation time between machines is fixed.
• Processing time includes the machine’s setup time.
• All machines are available from the start, and each job becomes available upon arrival.
• Each machine processes only one job at a time, and no processing operation can be interrupted.
This paper aims to minimize the average weighted tardiness of dynamic jobs as outlined in Eq:
$$
minimize\frac{1}{n} \sum_{i=1}^{n}w_it_i = \frac{1}{n} \sum_{i=1}^{n}w_iT_i = \frac{1}{n}w_imax(0,c_i-d_i)
$$
Heterogeneous multi-agent scheduling solutions
Heterogeneous multi-agent scheduling model
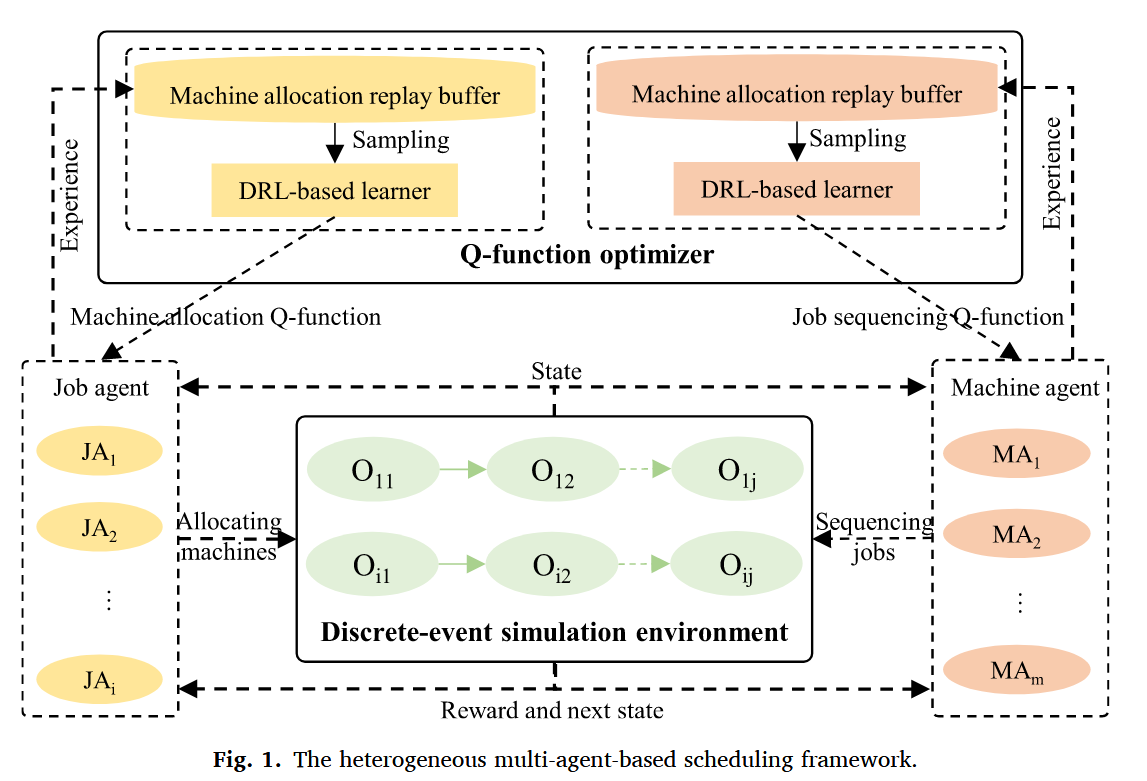
Heterogeneous multi-agent scheduling solutions
Observations of heterogeneous job and machine agents
$$
\begin{gather*}
s_t = \left{s_{ti}^{job} \mid i = 1,2,\ldots \right} \cup \left{s_{tk}^{mac} \mid k=1,2,\ldots,m \right},s_t \in S \
s_{ti}^{job} = \left{j,at_i,est_{ij},ro_{ij},arpt{ij},pt{ijk},w_i,d_i \right},\forall i \in J’ \
s_{tk}^{mac} = \left{crpt_t^k,trpt_t^k,nbj_t^k \right},\forall k \in M \
oja_t^i = \left{s_{tk}^{mac},pt_{ijk},tt_{M_{ij}}^k \mid k=1,2,\ldots,m \right} \
oma_t^k = \left{at_i,est_{ij},ro_{ij},pt_{ijk},w_i,d_i\mid i \in MB_t^k\right}
\end{gather*}
$$
$s_{ti}^{job}$describes the current operation, arrived time, earliest starting time, number of remaining operations, average remaining processing time, processing time on available machines, weight, and due date.
$s_{tk}^{mac}$indicating the current remaining processing time, total remaining processing time, and number of jobs in the buffer.
$oja_i^t$, includes data about machines, processing times, and transportation times.
$oma_t^k$, comprises details regarding the pending jobs in its queue.
Heterogeneous multi-agent scheduling solutions
Actions of heterogeneous job and machine agents

Heterogeneous multi-agent scheduling solutions
Actions of heterogeneous job and machine agents

Heterogeneous multi-agent scheduling solutions
Reward function with shaping
In DFJSP, job tardiness is unattainable until each job’s last operation is completed, which leads to sparse rewards for both the job and machine agent during the learning process.
In response, this paper proposes a reward-shaping mechanism that shares the reward for job completion between the job and machine agents involved in its processing. Upon completing a job, the weighted tardiness is calculated as defined in Eq. (19), which serves as the shared reward for both the job and machine agents involved in the completion process. Thus, the job agent directly receives a reward aligned with the optimization objective, rjatij, as outlined in Eq. (20). Likewise, this reward is distributed among machine agents, rmatijk, corresponding to the set of machines that completes the job’s operations, illustrated in Eq. (21).
$$
\begin{gather*}
wt_i = -w_iT_i = -w_imax\left{0,c_i,-d_i \right} \tag{19} &&\
rja_{tijk} = wt_i, \forall j \in [1,NO_i] \tag{20} &&\
rma_{tijk} = wt_i, if X_{ijk} = 1, \forall k \in [1,m] \tag21
\end{gather*}
$$
Heterogeneous multi-agent scheduling solutions
Heterogeneous multi-agent scheduling algorithm

Heterogeneous multi-agent scheduling solutions
Heterogeneous multi-agent scheduling algorithm

Heterogeneous multi-agent scheduling solutions
Heterogeneous multi-agent scheduling algorithm
